УДК 523.165+523.72                                                                                           ФИЗИКА

Г. Ф. КРЫМСКИЙ

РЕГУЛЯРНЫЙ МЕХАНИЗМ УСКОРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ НА ФРОНТЕ УДАРНОЙ ВОЛНЫ

(Представлено академиком С. Н. Верновым 18 X 1976)

В работах (1, 2) рассматривалось ускорение заряженных частиц на фронте ударной волны с регулярным магнитным полем. Основной результат, полученный в этих работах, состоит в том, что ускорение имеет «адиабатический» характер, т. е. набор энергии частицей ограничен в соответствии с тем, как это происходит при обычном адиабатическом сжатии магнитного поля с газом космических лучей.

 

Идея ускорения частиц в межпланетной среде базируется на том экспериментальном факте (3), что прохождение Земли через фронты межпланетных ударных волн сопровождается возрастаниями космических лучей низких энергий. По-видимому, первой работой, где был разработан конкретный механизм такого ускорения, была работа (4). В ней рассмотрено статистическое ускорение частиц на турбулентности за фронтом ударной волны. Вспышки космических лучей в августе 1972 г., ноябре 1968 г. и другие факты побуждают вернуться к рассмотрению «чистого» случая (сверхадиабатического) ускорения частиц на ударном фронте

 

Рассмотрим идеализированную задачу об ускорении частиц сильной ударной волной плоской геометрии, распространяющейся в среде, где содержатся маломасштабные нерегулярности магнитного поля, рассеивающие частицы. Будем считать среду однородной, а распространение ударной волны стационарным. В такой постановке фронт ударной волны разделяет два полупространства: x<0 и x>0. причем скорость среды

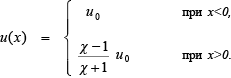
Пусть D(x,p) коэффициент диффузии частиц с импульсом р, а n(р, х) — плотность частиц, отнесенная к единичному интервалу ска­лярного импульса. Тогда можно воспользоваться равнением

полученным в работах (5, 8), для определения плотности ускоренных ча­стиц. Для нашей задачи с одномерной геометрией имеем в стационарном случае

Интегрируя уравнение по х, получаем

Функция Хэвисайда

Замечая, что «вверх по потоку» от фронта частицы далеко распространяться не могут (т. е. n¦_x→-∞→0) видим, что константа интегрирования С,=0. Производя повторное интегрирование убеждаемся, что ограниченное решение в правой области не зависит от расстояния и не зависит от конкретного вида функции D(x,p):

Для левой области получается экспоненциально убывающее от фронта решение, которое легко может быть найдено и здесь не выписывается. По­следнее соотношение можно рассматривать как дифференциальное урав­нение, определяющее зависимость плотности от импульса. Очевидно.

В случае идеального газа, χ=5/3 а в случае «сильного» магнитного поля χ=2. Показатель спектра соответственно у=2 и у =2,5, т. е. получаем жесткий энергетический спектр

Итак, мы получили механизм ускорения частиц на ударном фронте, который обеспечивает наблюдаемый спектр галактических космических лучей или даже более жесткий. Физический смысл механизма ускорения очевиден: частицы в результате рассеяний на нерегулярностях магнитного поля среды многократно могут пересекать область сжатия вещества в окрестностях фронта, прежде чем они будут унесены от фронта потоком вещества в возмущенную область. Можно ожидать, что рассмотренный механизм ускорения будет «уни­версальным», т. е. пригодным к ускорению частиц в системах различных масштабов. Для того чтобы ускорение космических лучей могло быть обе­спечено этим механизмом, необходимо выполнение некоторых дополнительных условий. Совершенно ясно по энергетическим соображениям, что механизм не должен действовать на все или на большую часть частиц. Это требование, по-видимому, выполняется довольно легко, так как ударный фронт не является бесконечно тонким. Толщина фронта «автоматически» устанавливается такой, чтобы основная часть частиц была лишена возмож­ности многократно пересекать фронт n, следовательно, подвергаться уско­рению. Лишь небольшая доля наиболее энергичных частиц сможет полу­чить дальнейшее ускорение. Механизм, регулирующий число ускоренных частиц, должен описываться нелинейным взаимодействием между колеба­ниями на фронте и отдельными частицами

 

Описанная выше модель предусматривала лишь один источник потерь частиц: их конвективный снос от фронта. В дополнение к нему могут иметь место потери за счет ухода частиц из области ускорения (конечные размеры системы), расширения ударных волн наружу и соответствующих эффектов замедления. Во всех этих случаях спектр ускоренных частиц должен быть мягче, чем определенный выше теоретически достижимый предел

 

 

 

Институт космофизических исследований и аэрономии                                               Поступило

Якутского филиала                                                                                                        6  X  1976

ЛИТЕРАТУРА

1. В. П. Шабанский, ЖЭТФ, т. 41, № 4 (10), 1107 (1961).
2. Л. И. Дорман, Ускорительные пропессы в космосе. «Итоги науки», сер. Астрономия, т. 7, М. 1972, стр. 233.
3. А. Н. Чарахчъян, УФН, т. 83, 35 (1964).
4. Б. А. Тверской, ЖЭТФ т. 53, 1417 (1967).
5. Е.N. Parker, Proc. Intern. Conf. on Cosmic Rays, v. 1. 1965, p. 26.
6. A. 3. Долгинов, И. Топтыгин Изв. АН СССР, сер. физ., т. 30, № 11, 1780 (1966)
7. J. Glesson, W. I. Axford Astrophys. J., v. 154, 1011 (1968).
8. Г. Ф. Крымский, Геомагнетизм и аэрономия, т. 4, № 6 (1964).
9. Г. Ф. Крымский, Модуляция космических лучей в межпланетном пространстве, «Наука», 1969